Unit V BQ # 7

The formula from the difference quotient comes from the graph we draw and the two sections that are f of x and x plus h. We put this all over h and that is how we get our difference quotient formula. Fromthe graph we pull the equation f of x plus x plus h all over h. This is the formula that we use in order to find the difference quotient.

Unit U BQ # 6

1.) A continuity is a predictable line, that contains absolutely no jumps, breaks, or holes in it. The line can also has to be able to be drawn without lifting one's pen/pencil off of the paper. On the other hand a Discontinuity is that of a point, jump, infinite, or oscillating. At a point discontinuity there is a difference in the limit and value of the function. When there is a jump discontinuity there is literally a jump in the graph, the graph stops at one point and then starts anew at another point. Infinite discontinuity occurs when there are vertical asymptotes in the function, this leads to unbounded behavior. Oscillating discontinuity occurs plain and simply because it is oscillating.

2.) A limit is the intended height that a function is intending on reaching, where as a value is the actual height that the function reaches. The limit exists at a point discontinuity because the line can still meet at the given point even if there is nothing there. The limit does not exist at the following: jump, infinite and oscillating discontinuity.

3.) One evaluates limits numerically through the use of a table. Graphically, it is as simple as making sure the graph meets at a given point. As far as solving the limit algebraically there is a number of ways to solve which include: direct substitution, dividing out, and rationalizing.  

BQ #4 Unit T Concept 3

Why is a normal Tangent graph uphill and a Cotangent graph downhill? Use the unit circle to explain.

The reason that tangent goes uphill when graphed and cotangent goes downhill when graphed is due to that fact that that they are reciprocals of each other. What this means is that when graphed what will happen to tangent the opposite will have to happen to cotangent. The other thing is that it is also based on its unit circle ratios, Tangent and Cotangent are +-+-, but Tangent is drawn from the Sine graph and Cotangent is graphed from the cosine graph line.

BQ#4 – Unit T Concepts 3 Why is a “normal” tangent graph uphill, but a “normal” Cotangent graph downhill?

Why is a “normal” tangent graph uphill, but a “normal” Cotangent graph downhill? Use unit circle ratios to explain.

The reason that tangent goes uphill when graphed and cotangent goes downhill when graphed is due to that fact that that they are reciprocals of each other. What this means is that when graphed what will happen to tangent the opposite will have to happen to cotangent. The other thing is that it is also based on its unit circle ratios, Tangent and Cotangent are +-+-, but Tangent is drawn from the Sine graph and Cotangent is graphed from the cosine graph line.

BQ#5 – Unit T Concepts 1-3

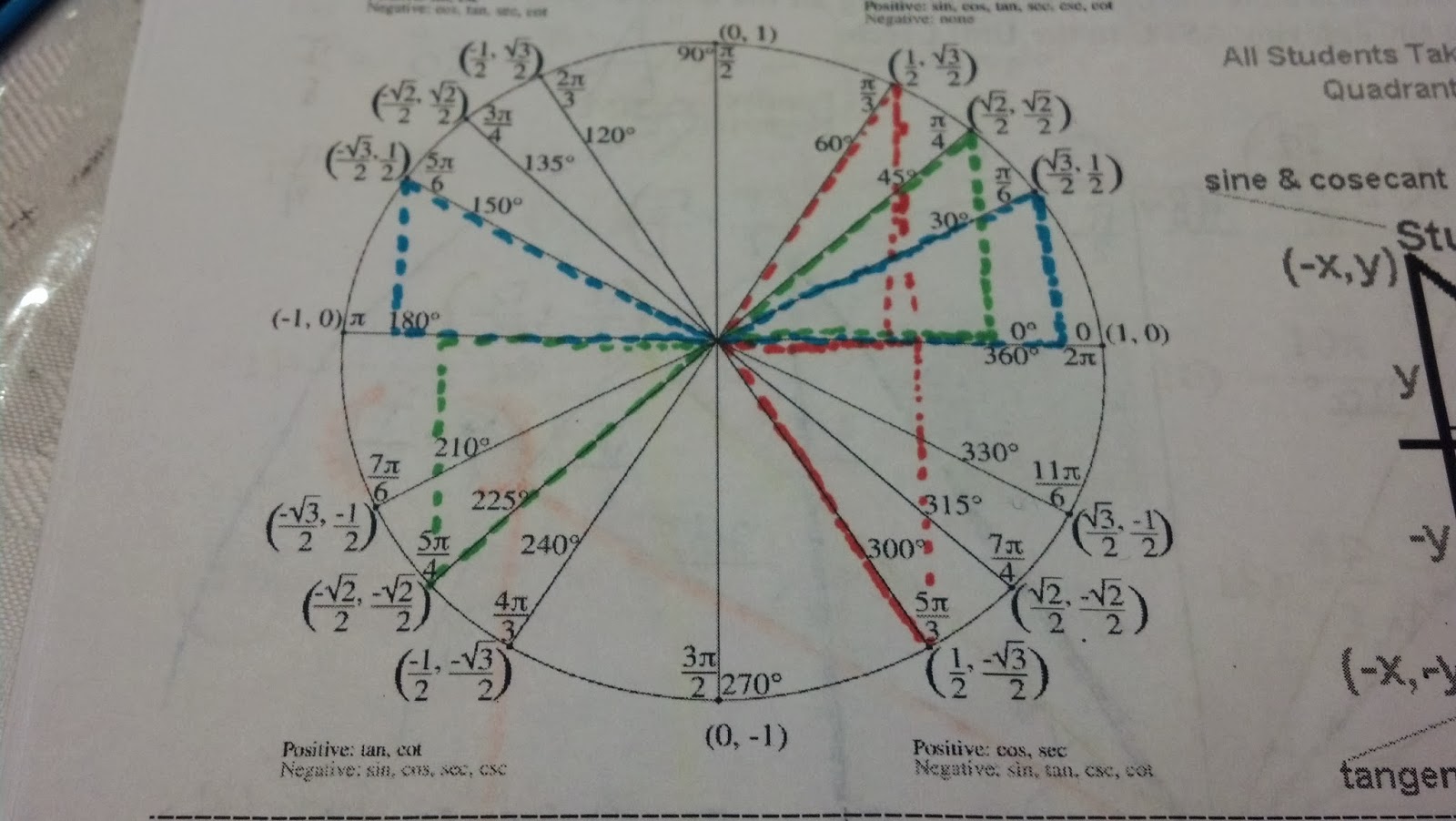
Sine and Cosine do not have asymptotes due to that fact that they simply move left and right and get smaller and bigger. The other four trig functions have asymptotes because they rely on the asymptotes to mark where they can start and end with their lines. This is because they move up and down, they also move left and right.
But most important ly is due to that fact that Sine and Cosine become undefined and thus create an asymptote when they are being used with the four other trig graphs.

BQ# 3: Unit T Concept 1-3 , How do the graphs of Sine and Cosine relate to each other?

How do the graphs of sine and cosine relate to each of the others?  Emphasize asymptotes in your response.

Sine and Cosine relate to each of the other graphs due to that fact that they serve as a stepping stone in a way. All the other graphs are based on these two lines that come from Sine and Cosine. Asymptotes are formed at the mark where cosine is equal to zero and sine is equal to one. All of the lines drawn are always close to but never touching the asymptote.

Tangent?

The lines are facing upwards in the graph they are going off by the points that are created by Sin and Cosine.

Cotangent? 

These lines are the exact opposite of Tangent. The reason for this is due to that fact that Cotangent is the reciprocal of Tangent so that is why the lines are facing in the opposite direction.

Secant?

Secant is a weird graph it is a set of parabolas in each period. Each asymptote has a part of the line that makes up the parabola in the end.

Cosecant?

These lines are the exact opposite of Secant. The reason for this is due to thatfact that it is the reciprocal of Secant, so that is why the lines are facing in the opposite direction.

Reflection#1 Verifying Trig Functions

1. To verify a trig function means to  fully simplify a trig function so that a said side is equal to another. 
2. The tips that I have found useful in this unit is to work with Sin and Cos as much as possible. The reason for this id due to the fact that these two trig function are the easiest to work with, that and sec squared and tan squared.
3. When verifying a trigonometric function look for what to do first: pull out a gcf, lcd, foil, etc. After this can the identities be replaced with sin and cos? Check for this. After this simply take it step by step and organize your work so that everything doesn't get mixed up. 

I/D #3 Unit Q Pythagorean Derivations

1. Where does where sin^2x+cos^2x=1 come from to begin with (think Unit Circle!). You should be referring to Unit Circle ratios and the Pythagorean Theorem in your explanation.

Sin^2x +cos^2x=1 comes from the Pythagorean Theorem. Since Sine is equal to y over r and that is eqaul to y^2. Cosine is equal to x over r, which in referring to the Pythagorean Theorem is eqaul to x^2. When you put this together you have x/r^2 + y/r^2 = 1 or sin^2x + cos^2x = 1.

When deriving the two remaining Pythagorean Theorems you have Tan^2theta +1 = Sec^2theta and 1 + Cot^2theta = Cosecant^2theta. For the first one you have tanx= sinx/cosx then you multiply tanx by tanx=sinx/cosx times sinx/cosx you will be left with Tan^2x = Sin^2x/Cos^2x. For the second one you will do the same but have One/tan and one/sin to work with instead of the other two.

2. The connections that I see between Units N, O, P, and Q so far are…

The connections that I see so far are that the unit circle expands so much farther than I thought. I see that the ratios of Sin,Cos, and Tan can be used in many numerous equations across the unit of trigonometry.

3. If I had to describe trigonometry in THREE words, they would be…

Difficult and Tedious

WPP # 13 & 14 Unit P Concept 6 and 7

This WPP post was made in collaboration with Joshua Nolasco. Please visit the other awesome posts found on their blog and our WPP by clicking here.

WPP # 12: Unit O Concept 10 Elevation and Depression Word Problem

A) Bob at ground level measures the angle of elevation to the top of the mountain's slope to be 70 degrees, if at this point Bob is 18 feet away from the building, what is the height of the mountain?

B) Bob now stands atop. He measures the angle depression from where he is now to the ski resort to be 48 degree. He knows that he is 700 feet higher than the base of the course. How long is the path that he will descend?

I/D #2 How can we derive the patterns from our special right triangles?

Inquiry Activity Summary

In class I completed a worksheet in which I had to find as to why and how I would find the special patterns of the two special right triangles. One of them being the thirty, sixty, ninety, and the other being the forty five forty five ninety triangle.

For the forty five, forty five, ninety triangle I drew a dotted line diagonally down the middle of the square. A square has a ninety degree angle cutting this down the middle creates a forty five degree angle. After you have done this you create the special triangle. Label your special triangle correctly. Label the shared side as Y, then label X . You are given a side length of one to work with. After you label both of your sides with the given, you use the Pythagorean Theorem to find the length of the hypotenuse. You should set this up as one squared plus one squared equals c squared, as an answer you should get radical two as an answer.  From this we derive the special pattern N, N, N radical 2. The reason for n is due to the fact that it can stand for any given value in the world.

For the thirty, sixty, ninety triangle I drew a dotted line straight down the middle of the triangle to split it in half. I label the shared line with Y and then I label X. You are given a side length of one to label the sides with.  When you do this you end up with the angles of thirty, sixty, and ninety. When this happens the side length that you were given of one changes to one half. You now have one and one half to work with for the Pythagorean Theorem You set it up with one squared plus b squared equals one half squared. You should end up with the answer of radical three over two for the side of Y. Now we can add N into the pattern. When we do this you can derive the special pattern you now have 2N, N, and N radical three. The reason for N is because it can stand for any number in the world, it has infinite values for it.

Inquiry Activity Reflection

Something I never noticed before about special right triangles is the N can stand for any value in the world.

Being able to derive these patterns myself aids in my learning because I can now fully understand how and where these patterns come from.

ID # 1: Unit N Concept 7 How do SRT and UC relate?

Inquiry Summary Activity
In class on Wednesday I completed a special triangle activity. The activity was based on the three types of special triangles that are found in math. Those three triangles are a thirty, sixty, and ninety degree triangle and the other one is a forty five, forty five, ninety degree triangle, the third ons is a varitation of the thirty sixty ninety triangle.

The thirty degree triangle is the one that matches up with the ordered pair of radical three over two and one half. It has a radian measure of pi over six.

The forty five degree triangle is the one that matches up with radical two over two and radical two over two. It has a radian measure of pi over four.

The sixty degree trianlge is the one that matches up with the ordered pair of one half and radical three over two.

This activity helps with the unit circle because these three triangles are what make up the unit circle. Once you find these three triangles you can find the other three quadrants of the circle. Simply add and simplify all the way around the circle.The triangle always has to be in the first quadrant. If you were to draw these triangles in any of the other quadrants the values of the degrees would go up, the radians would also increase, and lastly the ordered pairs would differ from positive and negative.

As you can see the radians change and the degrees go up according the the revolution of the circle, zero to three sixty. The thirty degree triangle is now at one hundred and fifty degrees with a radian measure of five pi over six, this being in the second quadrant. The forty five triangle is now at two hundred and twenty five degrees and has a radian measure of five pi over four, this being in the third quadrant. The sixty degree triangle is now at three hundred degrees and now has a radian measure of five pi over three, this being the fourth quadrant. Another thing to notice is how the ordered pairs transition from positive to negative according to the quadrant of the unit circle.

The coolest thing I learned from this activity was how by finding one part of the circle one can easily solve for the entire unit circle.
This activity will help me in this unit because I will be able to solve for the rest of the unit with ease or if not at least have a tool to refer to in case I get stuck with my work.
Something I never realized before about special right triangles and the unit circle is, this whole concept is new to me so its all pretty intresting.

RWA # 1 Unit M Concept 5 (Graphing ellipses given equations)

RWA Real World Conic Section Application

1. Ellipses - "the set of all points such that the sum of the distance from the points is a constant."
2. Algebraically- (x-h)^2/a^2 + (y-k)^2/b^2 = 1 is what the equation looks like. The ellipse looks like an odd shaped football, almost egg shaped at times, it all depends upon the eccentricity. The ellipse has two vertices, two co-vertices, two foci, a major axis, minor axis, and a center. One finds these major parts by completing the square and then filling in the spaces of the chart, or the other way around taking bits of the chart and working backwards to find the standard form equation.
3. "Ellipse (including the circle, for which you can find many examples in life) real-life examples/uses:  since an ellipse has two focii (plural of focus), rather than only one like a parabola, the ellipse makes a great whispering gallery, where one person can whisper at one focus, and someone at the other focus (which may be far away) can clearly hear it;  an ellipitical trainer, used to simulate running indoors, copies the ellipitical motion your foot normally makes when running; the shape many cooks cut foods into, to make them more attractive (like cucumbers, carrots, potatoes, and similar)"(http://www.wyzant.com/resources/answers/3187/conic_sections_application) The ellipse is used from what I have found above in the dixie cup walkie talkies kids make with string. Its quite funny how ellipses and other math properties play a huge role in eveyday life.
4. Find ellipse link here 
5. Find Video link here 
6. Find picture link here 
7. References
• (http://www.wyzant.com/resources/answers/3187/conic_sections_application)
• http://mathforum.org/library/drmath/view/62576.html
• http://www.youtube.com/watch?v=AVrUEAiw5gA&feature=youtu.be
• http://britton.disted.camosun.bc.ca/elliplanet_lg.JPG